Matlab教程笔记：第二章(上)

目录

Matlab变量与常量
Matlab基本数据结构
Matlab空数组与子数组
Matlab算数运算符
传统算数运算
 矩阵向量运算
 常见的Matlab运算函数
后续还需学习的知识
Reference

Matlab变量与常量

变量默认为double型，包括由64位双精度浮点数构成的标量或数组。 double为双精度，-10^308~10^308，15~16位有效数字，占4个字节。

变量名由字母，数字，下划线构成。弱类型语言，大小写敏感。

Matlab的数据类型如下图所示。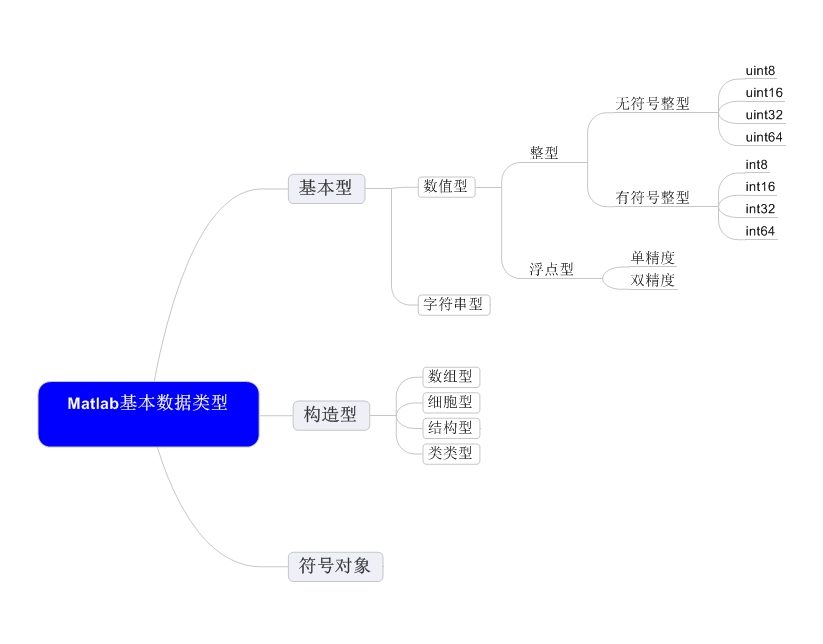

变量初始化方法如下:

赋值语句初始化
用input函数从键盘输入,通过help input指令可以查看input指令的详细信息。
R = input('how many apple')括号内表示提示信息。

matlab中的符号常量：

i或j为虚数单位
Inf或inf表示正无穷大
NaN表示不定式，非数值量，产生于0/0,无穷/无穷，0*无穷等运算
pi表示圆周率
eps,realmin,realmax分别表示Matlab中最小的浮点数精度，实数的最小值和最大值

这些常量的范围如下。
ans为Matlab内置的变量（系统保留的变量名）

Matlab基本数据结构

Matlab的基本数据结构有:标量，向量（数组），矩阵

Matlab中空格可以分开一行的数字，也可以用逗号分开数字，比如small = [1,2]，把逗号和空格混用也可以，但是这样看起来或者写起来会比较奇怪。

例如：

a=[1 2 3]表示一个行向量
b=[1 2 3]'表示一个列向量 (一个单引号，表示转置)
c=[1;2;3]也表示一个列向量 (列向量有不同的表示方法)

在Matlab中可以用内置函数生成矩阵：

ones(4)表示4*4的方阵，矩阵全部元素都为1
ones(4,3)第一个参数表示行，第二个参数表示列，矩阵全部元素都为1
zeros(5),zero(4,5)与上面的格式相同，只不过矩阵元素都为0
eye(5)表示5*5的单位矩阵,还有eye(2,3)，按照单位矩阵来填，其余元素均为0

eye()函数生成矩阵的示例如下：
![]/img/post3/2.jpg)
randi()函数可以用来生成随机数。rgn(0)可以用来设置随机的seed。

randi(IMAx,n)表示生成[1,IMAX]区间中的随机数，同时构造n*n的矩阵。
randi(IMAX,n,m,p,...)表示生成[1,IMAX]区间中的随机数，同时构造n*m*p*...的矩阵；也可以用这种形式rand(IMAX,[n,m,p,,,,])。
IMAX也可以替换成[A,B]表示生成[A,B]之间的随机数

冒号表达式生成矩阵：

j:k生成[j,j+1,...,k]的行向量 (j>k时生成空向量)
j:i:k生成[j,j+i,j+2*i,...,j+m*i] (j+m*i<=k)，(1:2:100)'表示由[1 3 5 ... 99]组成的列向量

l=(1:2:10)这样打上括号以后用冒号表达式产生的序列l实际是一个数组，这里l也是行向量
a(i)表示a数组的第i个元素
d(i,j)表示矩阵(i,j)位置处的数据，注意：Matlab中按照列来存储，不是按行存储
A(:,j)表示矩阵A的第j列全部元素，此时冒号代表所有元素
A(i,:)表示矩阵A的第i行全部元素

注意：Matlab的下标从1开始，而不是从0开始的，这与C语言中的语法有所不同
A(i:j,k)引用A[i][k]到A[j][k]的向量
- A(i:j)表示矩阵A的a[i][1]到a[j][1]这些元素构成的数组，第二维不写的话默认值为1，即第1列
A(i:j:k,l)定义了A[i][k]，A[i+j][k]，...A[i+m*j][k]组成的向量，其中i+m*j<=k
定义矩阵不能缺少元素，否则会出错

可以通过赋值语句定义矩阵。比如，k(2,3)=8结果如下

k=
   0 0 0
   0 0 8

Matlab中也可以用矩阵嵌套来生成矩阵。比如l=[k,k]以行的形式进行矩阵嵌套，结果如下：

l=
   0 0 0 0 0 0
   0 0 8 0 0 8

当然也可以执行l=[k;k]以列的形式进行矩阵嵌套。

此外，还有这样的矩阵表示方法。

>>l=[1:2:6;2 4 6]
%其中第一行为1 3 5，第二行为2 4 6

Matlab中的size函数通过这样的指令：size(A)(其中A代表二维矩阵)可以返回矩阵对应的行和列的维数

ans=
    2 3

当命令为[r,c]=size(A)时，即输出为两个元素的数组，则r代表矩阵的行数，c代表矩阵的列数。如果命令为size(A,n)的形式，则当n=1时，返回矩阵的行数，n=2时返回矩阵的列数。

length函数通过这样调用length(l)来返回一个矩阵行和列中最大的一个，所以这个指令的返回结果为3

如果矩阵比较大时，在workspace中输入矩阵名称，双击以后就可以像excel一样输入，十分方便

MatLab中的空数组和子数组

a=[]表示空矩阵。

b=magic(4)表示生成魔方矩阵，矩阵元素如下：

c=b(3,:)取出b矩阵第3行所有元素构成行向量
c=b(3,[2,4])取出b矩阵第3行的第2列和第4列的元素构成行向量，注意里面必须用[2,4]方括号，而不能用圆括号
c=b(3,2:end)取出b矩阵第3行的第2列直到最后一列的元素

在Matlab中，linspace函数以等差数列方式形成数组，logspace函数以等比数列方式形成数组。

linspace(x1,x2)默认返回100个x1到x2之间的数，包括x1和x2在内
linspace(x1,x2,N)返回N个x1到x2之间的数，N<2时返回x2，包括x1和x2在内
logspace(x1,x2)生成一个10^x1,到10^x2之间的50个数字，包括x1和x2在内
logspace(x1,x2，N)生成N个等比数列的元素，包括x1和x2在内

reshape函数将已知的数组或矩阵生成参数所设定的矩阵的形状

>> 1:1:9
%结果如下：
ans=
   1 2 3 4 5 6 7 8 9
>> reshape(ans,3,3)
%结果如下：
ans= 
   1 4 7
   2 5 8
   3 6 9

reshape(x,m,n)函数将x生成m*n维数组
reshape(x,m,n,p,...)函数将x生成m*n*p*…的高维数组

但是需要注意：resize(x,m,n,p,...)必须保证n*m*p*...=numel(x)，否则会报错,其中numel(x)函数用来表示矩阵x中元素的个数

这里再介绍几个Matlab的系统预定义变量：date,clock,year,month,now,today

date返回当前日期，按照日-月-年格式返回
clock返回当前的时间
year(now)返回当前的年，month(now)返回当前的月，day(now)返回当前的日，day(today)和day(now)结果相同

Matlab算数运算符

传统算数运算

算数除法

>> 5/6
ans=
   0.83333333333333

右除,第一个数字为除数，第二个为被除数

>> 5\6
ans=
   1.20000000000000

我用Matlab R2014b执行这两个命令，得到的结果都只保留了5位有效数字，和上面这个不一样。

5^2表示5的平方，power(5,2)也可以表示5的平方

传统算数运算中的中括号，大括号在Matlab中都用小括号替代，比如算式3*(5*(4+6)),因此在计算时需要注意运算符的优先级，在合适的地方恰当地使用小括号。

矩阵向量运算

矩阵加法，减法，乘法，除法四种运算对应==> + - * / \五个符号

矩阵除法相当于A与B的逆矩阵相乘。所以A/B=A*inv(B)等式成立，其中inv(B)表示B的逆矩阵。
矩阵也可以右除，有该等式成立A\B=inv(A)*B
矩阵乘方运算，A^3表示三个A矩阵连续做矩阵乘法，而不是矩阵元素的三次幂

Matlab区分数组和矩阵，在相应的运算符前加点.符号。

A.*B表示A中对应位置的元素和B中对应位置的元素相乘。和A*B严格按照矩阵乘法运算不同。

>> a=[1 2 3]
>> b=[1 2 3]'
>> a.*b %这样会出错，因为a和b对应位置不同

当A为矩阵时，

A.^3就表示每个位置上的数字做相应的乘方运算
A./3就表示每个位置上的数字除以3
A.\3就表示每个位置上的数字被3除
A+3表示A中每个元素都加上3
A.+3就会出现错误

常见Matlab运算函数

sin()函数参数为弧度值，sin(A)中A为矩阵时，相当于对A矩阵中每个元素求其sin的值。
log()对数函数以e为底，log2()对数函数以2为底，log10()对数函数以10为底。
abs()函数为绝对值函数，sqrt()函数为开根号运算，sign()函数为取符号函数。
ceil()函数为向上取整函数，floor()函数为向下取整函数，fix()函数表示向0取整函数，round()函数表示向最近的整数取整，按照四舍五入规则。

round(-3.5)=-4对绝对值四舍五入。
mod()和rem()都为取模运算函数mod(-5,3)=-2，rem(-5,3)=1。注意根据实际需要选择合适的取模函数
conv(u,v)函数和deconv(u,v)函数可以计算多项式乘法和除法，其中u和v都为多项式，对多项式系数按照降幂排列。

Matlab中的conv和deconv函数不仅可以用于多项式的乘除运算，还可以用于两个有限长序列的卷积和解积运算。

Matlab提供的函数conv，语法格式：w=conv(u，v)，其中u和v分别是有限长度序列向量，w是u和v的卷积结果序列向量。如果向量u和v的长度分别为N和M，则向量w的长度为N+M-1.如果向量u和v是两个多项式的系数，则w就是这两个多项式乘积的系数。对于卷积运算的细节可以参考这篇博客。
sum()函数为求和函数，prob()函数为求积函数，max()函数为取最大值函数，min()函数为取最小值函数

若A为矩阵，max(A)求出的是每一列的最大值组成一个行向量。 max(max(A))就可以找到矩阵中的最大的元素

[Y,I]=max(X)返回矩阵或向量的最大值和它对应的下标
median(a)返回向量中的中值，median(A)返回向量中的第一个不是1的维度的中值组成的向量,median(A,DIM)表示顺着A矩阵第DIM个维度来求得的整个矩阵的中值行向量

例子：A=[1 2 4 4;3 4 6 6;5 6 8 8;5 6 8 8]; 这是一个4*4的矩阵，默认从第一个非1的维度求解，此时从第一维求解。即从水平方向看，求出每一列的中值然后组成行向量，即median(A)=[4 5 7 7],如果是median(A,2)则相当于是从竖直方向看，求出每一行的中值然后组成列向量，即median(A,2)=[3 5 7 7]'，注意此时生成的是列向量。
mean()函数为取平均值函数，用法及参数和median()函数大致相同
real()函数表示求解复数的实部；imag()函数表示求解复数的虚部；abs()函数表示求解复数的模；angle()函数表示求解复数的辐角；conj()函数表示取复数的共轭复数，和复数加一个引号’的用法一样。
cross(a,b)函数对矩阵做叉积；dot函数对向量做点积；compan函数生成多项式的伴随矩阵，不能用它来直接求矩阵的伴随矩阵；inv表示求矩阵的逆矩阵；det函数表示求矩阵的行列式；rank函数求矩阵的秩；trace函数求矩阵的迹；eig函数求解矩阵的特征值。

需要注意cross(A,B)中的A和B均为向量时，A和B的长度都必须为3，否则就会报错，此时函数返回A和B向量的叉积。

当A和B为矩阵或高维数组时，必须保证A和B的每个维度的大小都相同，此外所有维度中必须保证至少有一个维度为3，该函数会将A和B看成是有多个3维向量组成的数组，然后求出对应的3维向量做叉积后形成的矩阵。

后续还需学习的知识

弄清楚Matlab数据类型中构造型和符号对象的具体用法和细节
之后还需要继续学习Matlab的相关语法，熟悉矩阵和向量操作
记着翻阅别的博客中关于Matlab的conv函数介绍，在以后会比较多地使用该函数进行卷积操作等。

Reference

Matlab视频教程

http://www.51zxw.net/list.aspx?page=3&cid=456