目录
K-Means聚类算法
K-Means算法的伪代码如下所示:
创建k个点作为起始质心(经常是随机选择)
当任意一个点的簇分配结果发生改变时
对数据集中的每个数据点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将其均值作为质心
import kMeans
from numpy import *
dataMat = mat(kMeans.loadDataSet('testSet.txt'))
min(dataMat[:,0])
matrix([[-5.379713]])
min(dataMat[:,1])
matrix([[-4.232586]])
max(dataMat[:,1])
matrix([[ 5.1904]])
max(dataMat[:,0])
matrix([[ 4.838138]])
kMeans.randCent(dataMat, 2)
matrix([[ 1.0720982 , 0.98540353],
[ 1.03571702, -1.62238603]])
kMeans.distEclud(dataMat[0], dataMat[1])
5.184632816681332
reload(kMeans) #注意在写kMeans的时候,重新计算centroid的循环与计算每个点最近质心的循环平级,而不是嵌套(即注意缩进)
<module 'kMeans' from 'kMeans.pyc'>
dataMat = mat(kMeans.loadDataSet('testSet.txt'))
myCentroids, clustAssing = kMeans.kMeans(dataMat, 4)
m = 80
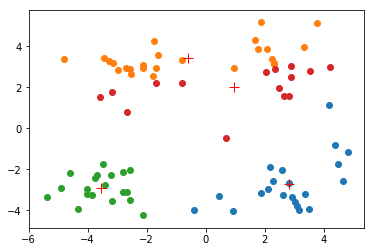
[[ 2.81706052 -2.71370657]
[-0.59512872 3.44969212]
[-3.53973889 -2.89384326]
[ 0.97906193 2.00484353]]
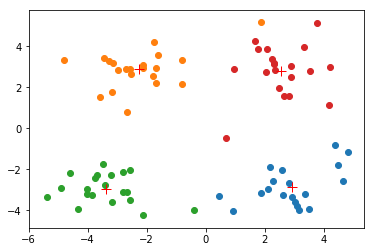
[[ 2.91339042 -2.85004268]
[-2.25437281 2.90180529]
[-3.38237045 -2.9473363 ]
[ 2.56728815 2.8251861 ]]
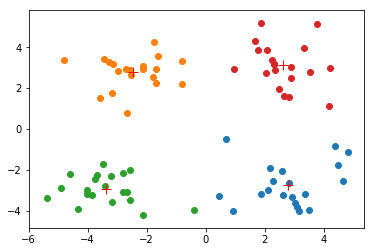
[[ 2.80293085 -2.7315146 ]
[-2.46154315 2.78737555]
[-3.38237045 -2.9473363 ]
[ 2.6265299 3.10868015]]
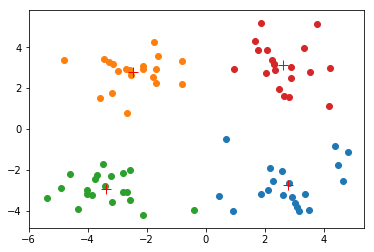
[[ 2.80293085 -2.7315146 ]
[-2.46154315 2.78737555]
[-3.38237045 -2.9473363 ]
[ 2.6265299 3.10868015]]
numIt = 4
print shape(dataMat)
(80, 2)
print shape(dataMat[:,0].flatten())
(1, 80)
dataMat[:,0].flatten().A[0]
array([ 1.658985, -3.453687, 4.838138, -5.379713, 0.972564, -3.567919,
0.450614, -3.487105, 2.668759, -3.156485, 3.165506, -2.786837,
4.208187, -2.123337, 0.704199, -0.39237 , 2.831667, -0.790153,
2.943496, -3.195883, 2.336445, -1.786345, 2.190101, -3.403367,
1.778124, -1.688346, 2.592976, -4.007257, 2.257734, -2.679011,
0.939512, -3.674424, 2.046259, -3.18947 , 4.372646, -2.579316,
1.889034, -0.798747, 2.83652 , -3.837877, 2.096701, -2.709034,
3.367037, -2.121479, 2.329546, -3.284816, 3.091414, -3.762093,
3.542056, -1.736822, 2.127073, -4.323818, 3.792121, -4.786473,
2.624081, -4.009299, 2.493525, -2.513661, 1.864375, -3.171184,
2.89422 , -2.562539, 3.491078, -2.565729, 3.332948, -1.616805,
2.280615, -2.651229, 2.321395, -1.685703, 3.031012, -4.599622,
4.196223, -2.133863, 4.668892, -2.793241, 2.884105, -2.967647,
4.479332, -4.905566])
myCentroids
matrix([[ 2.80293085, -2.7315146 ],
[-2.46154315, 2.78737555],
[-3.38237045, -2.9473363 ],
[ 2.6265299 , 3.10868015]])
myCentroids[:,0].flatten().A[0]
array([ 2.80293085, -2.46154315, -3.38237045, 2.6265299 ])
myCentroids[:,1].flatten().A[0]
array([-2.7315146 , 2.78737555, -2.9473363 , 3.10868015])
使用后处理提高聚类性能
K-Means算法会收敛,但聚类效果也可能会较差。原因是K-Means算法收敛到了局部最小值,而非全局最小值。
一种用于度量聚类效果的指标是SSE(Sum of Squared Error, 误差平方和),对应代码kMeans.py中kMeans函数的clusterAssment矩阵的第二列之和。
SSE值越小表示数据点越接近它们的质心,聚类效果也越好。因为对误差取了平方,所以更重视那些远离中心的点。
一种肯定能降低SSE的方法是增加簇的个数,但这会违背聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
对于K-Means算法陷入局部最小值的情况,有以下的改进方法。可以对生成的簇进行后处理,将具有最大SSE值的簇划分成两个簇。(具体实现时可以将最大簇包含的点过滤出来,然后再上面继续运行K-Means,k值取2)
为保持簇总数不变,我们可以合并两个簇。有两种可以量化的方法:合并最近的质心,或者合并两个使得SSE增幅最小的质心。第一种方法通过计算所有质心之间的距离,然后合并距离最近的两个点来实现。第二种方法需要合并两个簇然后计算总的SSE值,但这种方法需要尝试所有可能的两个簇,不断重复该处理过程,直到找到合并最佳的两个簇为止。
二分K-Means算法
该算法的提出是为了改进K-Means算法。
该算法首先将所有点作为一个簇,然后将该簇一分为二。之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复,直到得到用户指定的簇数目为止。另一种做法是选择SSE最大的簇进行划分,直到簇数目达到用户指定的数目为止。
二分K-Means算法的伪代码如下:
将所有点看成一个簇
当簇数目小于k时
对于每一个簇
计算总误差
在给定的簇上面进行K-Means聚类(k=2)
计算该簇一分为二之后的总误差
选择使得误差最小的那个簇进行划分操作
reload(kMeans)
<module 'kMeans' from 'kMeans.pyc'>
dataMat3 = mat(kMeans.loadDataSet('testSet2.txt'))
centList, myNewAssments = kMeans.biKmeans(dataMat3, 3)
centList: [[-0.15772275000000002, 1.2253301166666664]]
-------------------
m = 60
[[-2.71560067 3.37937762]
[ 1.21959613 0.06545838]]
[[-2.94737575 3.3263781 ]
[ 1.23710375 0.17480612]]
[[-2.94737575 3.3263781 ]
[ 1.23710375 0.17480612]]
numIt = 3
sseSplit, and notSplit: 570.722757425 0.0
the bestCentToSplit is: 0
the len of bestClustAss is: 60
[matrix([[-2.94737575, 3.3263781 ]]), matrix([[ 1.23710375, 0.17480612]])]
-------------------
m = 20
[[-3.5939405 1.451088 ]
[-2.87553522 3.53474367]]
[[-3.5939405 1.451088 ]
[-2.87553522 3.53474367]]
numIt = 2
sseSplit, and notSplit: 29.319041891 532.659806789
m = 40
[[-0.45965615 -2.7782156 ]
[ 2.93386365 3.12782785]]
[[-0.45965615 -2.7782156 ]
[ 2.93386365 3.12782785]]
numIt = 2
sseSplit, and notSplit: 68.6865481262 38.0629506357
the bestCentToSplit is: 1
the len of bestClustAss is: 40
[matrix([[-2.94737575, 3.3263781 ]]), matrix([[-0.45965615, -2.7782156 ]]), matrix([[ 2.93386365, 3.12782785]])]
centList
[matrix([[-2.94737575, 3.3263781 ]]),
matrix([[-0.45965615, -2.7782156 ]]),
matrix([[ 2.93386365, 3.12782785]])]
centList[0][:,0]
matrix([[-2.94737575]])