目录
1. 标准回归函数拟合
2. 局部线性回归法
3. 预测鲍鱼年龄
4. 解决特征维数比样本数大的问题
4.1. 岭回归
4.2. lasso方法
4.3. 前向逐步回归法
5. balance bias and variance
6. 预测乐高玩具价格
标准回归函数拟合
import regression
import numpy as np
xArr, yArr = regression.loadDataSet('ex0.txt')
xArr[0:2]
[[1.0, 0.067732], [1.0, 0.42781]]
yArr[0:2]
[3.176513, 3.816464]
ws = regression.standRegres(xArr, yArr)
ws
matrix([[ 3.00774324],
[ 1.69532264]])
xMat = np.mat(xArr)
yMat = np.mat(yArr)
yHat = xMat*ws
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0], yMat.T[:,0].flatten().A[0])
<matplotlib.collections.PathCollection at 0x836cf70>
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy * ws
ax.plot(xCopy[:,1], yHat)
[<matplotlib.lines.Line2D at 0x836cdd0>]
plt.show()
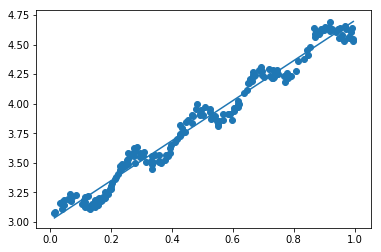
yHat = xMat * ws
np.corrcoef(yHat.T, yMat) #yHat和yMat的相关系数为0.98
array([[ 1. , 0.98647356],
[ 0.98647356, 1. ]])
局部线性回归法
xArr, yArr = regression.loadDataSet('ex0.txt')
yArr[0]
3.176513
regression.lwlr(xArr[0], xArr, yArr, 1.0)
matrix([[ 3.12204471]])
regression.lwlr(xArr[0], xArr, yArr, 0.001)
matrix([[ 3.20175729]])
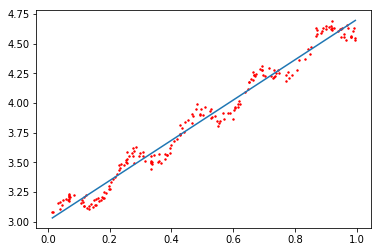
yHat = regression.lwlrTest(xArr, xArr, yArr, 1.0)
regression.drawFigure(xArr, yArr, yHat)
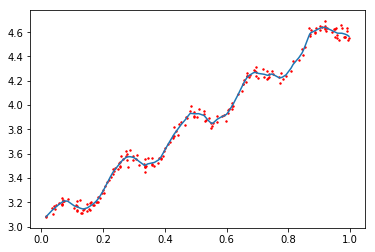
yHat = regression.lwlrTest(xArr, xArr, yArr, 0.01)
regression.drawFigure(xArr, yArr, yHat)
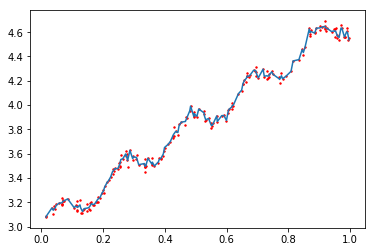
yHat = regression.lwlrTest(xArr, xArr, yArr, 0.003)
regression.drawFigure(xArr, yArr, yHat)
预测鲍鱼年龄
abX, abY = regression.loadDataSet('abalone.txt')
yHat01 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
yHat1 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
yHat10 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
reload(regression)
<module 'regression' from 'regression.pyc'>
regression.rssError(abY[0:99], yHat01.T)
56.790348630125777
regression.rssError(abY[0:99], yHat1.T)
429.89056187011255
regression.rssError(abY[0:99], yHat10.T)
549.11817088275757
使用小的核函数得到的误差较低,会使得训练误差变小,但容易过拟合。
yHat01 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
yHat1 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
yHat10 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
regression.rssError(abY[100:199], yHat01.T)
34763.549819890402
regression.rssError(abY[100:199], yHat1.T)
573.52614418940152
regression.rssError(abY[100:199], yHat10.T)
517.57119053826784
从上面看出kernel size = 10时测试误差最小,在训练集上误差最大
ws = regression.standRegres(abX[0:99], abY[0:99])
yHat = np.mat(abX[100:199]) * ws
regression.rssError(abY[100:199], yHat.T.A)
518.63631532417139
解决特征维数比样本数大的问题
在这种情况下,不能使用之前的方法。因为在求$(X^{T}X)^{-1}$的时候出错,矩阵是奇异矩阵,无法求逆。
岭回归
岭回归原理是在矩阵$X^{T}X$上加一个$\lambda I$使得矩阵非奇异,进而能对$X^{T}X+\lambda I$求逆。则新的回归系数计算公式变为如下:
岭回归最先用来处理特征数多于样本数的情况,现在也用于在估计中加入偏差,从而得到更好的估计。这里通过引入$\lambda$来限制所有w之和,通过引入该惩罚项,能够减少不重要的参数,这种技术在统计学中称为缩减(shrinkage)。
岭回归需要对数据xMat和yMat都进行归一化(可以减均值除以方差)
reload(regression)
<module 'regression' from 'regression.pyc'>
abX, abY = regression.loadDataSet('abalone.txt')
ridgeWeights = regression.ridgeTest(abX, abY)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeights) #这里之所以显示8条线,原因是ax.plot在绘制2-D mat的时候,将会按列进行绘制
plt.show()
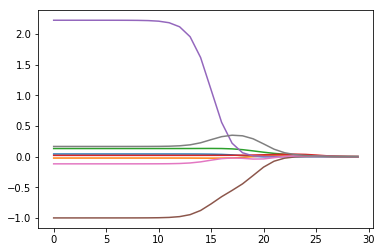
print np.shape(ridgeWeights)
(30, 8)
lasso方法
lasso方法与岭回归方法的不同之处在于,岭回归相当于在求cost function的时候加上了w的平方项约束。
而lasso的约束条件将平方和换成了绝对值,即
在$\lambda$足够小的时候,一些系数被迫缩减到0,这个特性可以帮助我们更好地理解数据。
前向逐步回归法
该算法可得到与lasso差不多的效果,贪心算法(每一步都尽可能减少误差)。初始权重均为1,然后每步决策是对某个权重增加或减少一个很小的值。
伪代码如下:
数据标准化(使其分布满足0均值,单位方差)
在每轮迭代过程中:
设置当前最小误差lowestError为正无穷
对每个特征:
增大或缩小:
改变一个系数得到一个新的W
计算新W下的误差
如果误差Error小于当前最小误差lowestError:设置Wbest等于当前W
将W设置为新的Wbest
reload(regression)
<module 'regression' from 'regression.pyc'>
xArr, yArr = regression.loadDataSet('abalone.txt')
regression.stageWise(xArr, yArr, 0.01, 200) #步长太大,w0在0.04和0.05之间震荡
[[ 5.06631554]
[-2.93368446]
[-0.93368446]
...,
[-0.93368446]
[ 0.06631554]
[ 2.06631554]]
--------------
[[ 0. 0. 0. 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.01 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.02 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.03 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.04 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.05 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.06 0. 0. 0. 0. ]]
[[ 0. 0. 0.01 0.06 0. 0. 0. 0. ]]
[[ 0. 0. 0.01 0.06 0. 0. 0. 0.01]]
[[ 0. 0. 0.01 0.06 0. 0. 0. 0.02]]
...
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.05 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.05 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.05 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.05 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
array([[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
...,
[ 0.05, 0. , 0.09, ..., -0.64, 0. , 0.36],
[ 0.04, 0. , 0.09, ..., -0.64, 0. , 0.36],
[ 0.05, 0. , 0.09, ..., -0.64, 0. , 0.36]])
regression.stageWise(xArr, yArr, 0.001, 5000)
[[ 5.06631554]
[-2.93368446]
[-0.93368446]
...,
[-0.93368446]
[ 0.06631554]
[ 2.06631554]]
--------------
[[ 0. 0. 0. 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.001 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.002 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.003 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.004 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.005 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.006 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.007 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.008 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.009 0. 0. 0. 0. ]]
...
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.043 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.043 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.043 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.043 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
array([[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
...,
[ 0.043, -0.011, 0.12 , ..., -0.963, -0.105, 0.187],
[ 0.044, -0.011, 0.12 , ..., -0.963, -0.105, 0.187],
[ 0.043, -0.011, 0.12 , ..., -0.963, -0.105, 0.187]])
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
xMat = regression.regularize(xMat)
yM = np.mean(yMat, 0)
yMat = yMat - yM
weights = regression.standRegres(xMat, yMat.T)
weights.T #可见5000次迭代之后,逐步线性回归法与常规最小二乘法效果类似
matrix([[ 0.0430442 , -0.02274163, 0.13214087, 0.02075182, 2.22403814,
-0.99895312, -0.11725427, 0.16622915]])
weights = regression.stageWise(xArr, yArr, 0.005, 1000)
[[ 5.06631554]
[-2.93368446]
[-0.93368446]
...,
[-0.93368446]
[ 0.06631554]
[ 2.06631554]]
--------------
[[ 0. 0. 0. 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.005 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.01 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.015 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.02 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.025 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.03 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.035 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.04 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.045 0. 0. 0. 0. ]]
...
[[ 0.04 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.045 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.04 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.045 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.04 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.045 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.04 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.045 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
[[ 0.04 0. 0.105 0.025 1.295 -0.83 -0.06 0.26 ]]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(weights)
plt.show()
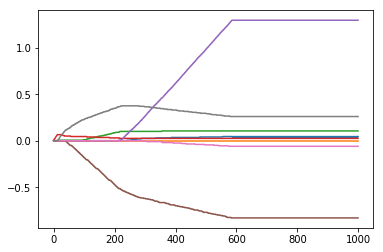
逐步线性回归法的一个好处是构建了模型之后,便于运行该算法找出重要的特征,这样就有可能及时停止对不重要特征的收集。
应用这种缩减方法(岭回归或者逐步线性回归)会使模型增加bias(偏差),减少variance(方差)。
balance bias and variance
训练误差和测试误差由三个部分组成:偏差,测量误差和随机噪声。第2节和第3节通过引入3个越来越小的核不断增大模型方差。第4节的缩减法将一系列系数缩减成很小的值或直接缩减为0,这样会增大模型的偏差。
方差是模型之间的差异(模型之间参数的差异),偏差是模型预测值和真实值之间的差异
预测乐高玩具价格
lgX = []
lgY = []
reload(regression)
<module 'regression' from 'regression.pyc'>
貌似API网址已经无法使用了,在使用urllib2.urlopen的时候会报错