目录
1. 决策树的构造
1.1. 信息增益
1.2. 划分数据集
1.3. 递归构建决策树
2. 在Python中使用Matplotlib注解绘制树形图
3. 测试和存储分类器
4. 示例:使用决策树预测隐形眼镜类型
决策树的构造
决策树的优缺点
- 优点:计算复杂度不高,输出结果易于理解,对中间值缺失不敏感,可以处理不相关特征数据。
- 缺点:可能会产生过度匹配的问题。
- 适用的数据类型:数值型和标称型。
在构造决策树时,需要解决的第一个问题就是,当前数据集上哪个特征在划分数据分类时起决定性作用。
创建分支的伪代码函数createBranch()如下所示:
检测数据集中每个子项是否属于同一分类:
if so
return 类标签
else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for 每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
return 分支节点
决策树的一般流程
(1) 收集数据:可以使用任何方法。
(2) 准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
(3) 分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
(4) 训练算法:构造树的数据结构。
(5) 测试算法:使用经验树计算错误率。
(6) 使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
本章采用的决策树算法是ID3算法,用它来划分数据集,该算法处理如何划分数据集,何时停止划分数据集。每次划分数据集时我们只选取一个特征属性。
信息增益
划分数据集的大原则是:将无序的数据变得更加有序。
在划分数据集之前之后信息发生的变化称为信息增益。对于每个特征而言,划分数据集之后获得信息增益最高的特征就是最好的选择。
熵(entropy)定义为信息的期望值。如果待分类的事务可能划分在多个分类中,则符号$x_{i}$的信息定义为:
其中,$p(x_{i})$是选择该分类的概率。
信息熵是所有类别所有可能值包含的信息期望值,公式如下:
其中n是分类的数目。
import trees
myDat, labels = trees.createDataSet()
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
labels
['no surfacing', 'flippers']
trees.calcShannonEnt(myDat)
0.9709505944546686
myDat[0][-1] = 'maybe'
myDat
[[1, 1, 'maybe'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
trees.calcShannonEnt(myDat)
1.3709505944546687
另一个度量集合无序程度的方法是基尼不纯度(Gini impurity) ,简单地说就是从一个数据集中随机选取子项,度量其被错误分类到其他分组里的概率。
划分数据集
a = [1,2,3]
b = [4,5,6]
a.append(b)
a
[1, 2, 3, [4, 5, 6]]
a = [1,2,3]
a.extend(b)
a
[1, 2, 3, 4, 5, 6]
reload(trees)
<module 'trees' from 'trees.pyc'>
myDat, labels = trees.createDataSet()
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
trees.splitDataSet(myDat, 0, 0)
[[1, 'no'], [1, 'no']]
trees.splitDataSet(myDat, 0, 1)
[[1, 'yes'], [1, 'yes'], [0, 'no']]
信息增益是熵的减少或者是数据无序度的减少。
reload(trees)
<module 'trees' from 'trees.pyc'>
myDat, labels = trees.createDataSet()
trees.chooseBestFeatureToSplit(myDat)
0
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
递归构建决策树
从数据集构造决策树的工作原理如下:
得到原始数据集,然后基于最好的属性值划分数据集,由于特征值可能多于两个,因此可能存在大于两个分支的数据集划分。第一次划分后,数据将被向下传递到树分支的下一个节点,在这个节点上,我们可以再次划分数据。
递归结束的条件是:
程序遍历完所有划分数据集的属性,或者每个分支下的所有实例都具有相同的属性。
第一个结束条件使得算法可以终止,我们甚至可以设置算法可以划分的最大分组数目。后续章节介绍的其他决策树算法如C4.5和CART算法,在运行时并不总是在每次划分分组时都会消耗特征。由于特征数目并不是在每次划分数据分组时都减少,因此这些算法在实际使用时可能引起一定的问题。
类标签不唯一时采用多数表决的方法来确定该叶子节点的分类。
reload(trees)
<module 'trees' from 'trees.pyc'>
myDat, labels = trees.createDataSet()
myTree = trees.createTree(myDat, labels)
myTree
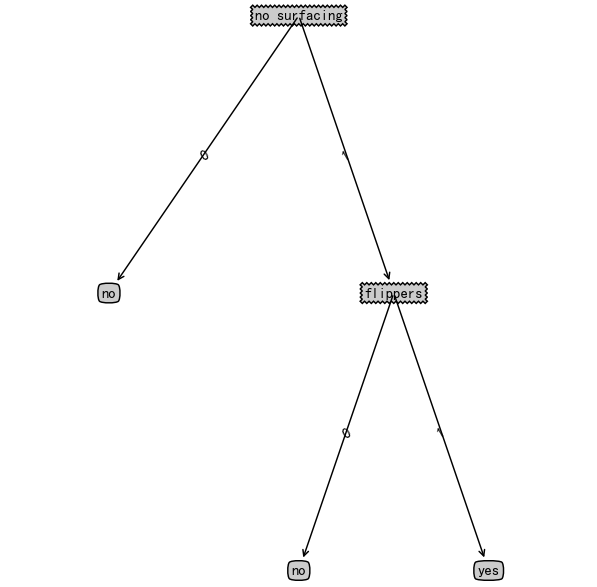
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
在Python中使用Matplotlib注解绘制树形图
Matplotlib库提供了一个注解工具annotations,可以在数据图形上添加文本注释。
注解通常用于解释数据的内容。
import treePlotter
reload(treePlotter)
<module 'treePlotter' from 'treePlotter.pyc'>
treePlotter.createPlotOrigin()
yes
create
create 1
这里在使用matplotlib的annotation的时候出现了中文乱码,在代码中加入以下两行之后,添加了对应的字体就可以找到中文了。
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
treePlotter.retrieveTree(1)
{'no surfacing': {0: 'no',
1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
myTree = treePlotter.retrieveTree(0)
treePlotter.getNumLeafs(myTree)
3
treePlotter.getTreeDepth(myTree)
2
绘制图形的x轴有效范围是0.0到1.0,y轴有效范围是0.0到1.0。
treePlotter.createPlot(myTree)
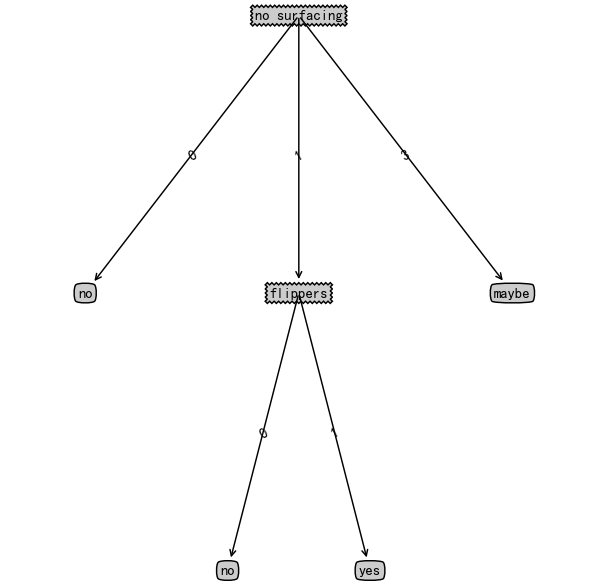
myTree['no surfacing'][3] = 'maybe'
myTree
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}, 3: 'maybe'}}
reload(treePlotter)
<module 'treePlotter' from 'treePlotter.pyc'>
treePlotter.createPlot(myTree)
测试和存储分类器
myDat, labels = trees.createDataSet()
labels
['no surfacing', 'flippers']
myTree = treePlotter.retrieveTree(0)
myTree
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
trees.classify(myTree, labels, [1,0])
'no'
trees.classify(myTree, labels, [1,1])
'yes'
构造决策树非常耗时,为了节省计算时间,最好能够在每次执行分类时调用已经构造好的决策树。使用Python的pickle模块序列化对象,可以快速读取保存在磁盘上的对象。
trees.storeTree(myTree, 'classifierStorage.txt')
trees.grabTree('classifierStorage.txt')
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
训练好的决策树可以保存在磁盘上,这也是其优点之一,k-近邻算法就无法持久化分类器。
示例:使用决策树预测隐形眼镜类型
fr = open('lenses.txt')
lenses = [inst.strip().split('\t') for inst in fr.readlines()]
lenses
[['young', 'myope', 'no', 'reduced', 'no lenses'],
['young', 'myope', 'no', 'normal', 'soft'],
['young', 'myope', 'yes', 'reduced', 'no lenses'],
['young', 'myope', 'yes', 'normal', 'hard'],
['young', 'hyper', 'no', 'reduced', 'no lenses'],
['young', 'hyper', 'no', 'normal', 'soft'],
['young', 'hyper', 'yes', 'reduced', 'no lenses'],
['young', 'hyper', 'yes', 'normal', 'hard'],
['pre', 'myope', 'no', 'reduced', 'no lenses'],
['pre', 'myope', 'no', 'normal', 'soft'],
['pre', 'myope', 'yes', 'reduced', 'no lenses'],
['pre', 'myope', 'yes', 'normal', 'hard'],
['pre', 'hyper', 'no', 'reduced', 'no lenses'],
['pre', 'hyper', 'no', 'normal', 'soft'],
['pre', 'hyper', 'yes', 'reduced', 'no lenses'],
['pre', 'hyper', 'yes', 'normal', 'no lenses'],
['presbyopic', 'myope', 'no', 'reduced', 'no lenses'],
['presbyopic', 'myope', 'no', 'normal', 'no lenses'],
['presbyopic', 'myope', 'yes', 'reduced', 'no lenses'],
['presbyopic', 'myope', 'yes', 'normal', 'hard'],
['presbyopic', 'hyper', 'no', 'reduced', 'no lenses'],
['presbyopic', 'hyper', 'no', 'normal', 'soft'],
['presbyopic', 'hyper', 'yes', 'reduced', 'no lenses'],
['presbyopic', 'hyper', 'yes', 'normal', 'no lenses']]
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
lensesTree = trees.createTree(lenses, lensesLabels)
lensesTree
{'tearRate': {'normal': {'astigmatic': {'no': {'age': {'pre': 'soft',
'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}},
'young': 'soft'}},
'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses',
'presbyopic': 'no lenses',
'young': 'hard'}},
'myope': 'hard'}}}},
'reduced': 'no lenses'}}
treePlotter.createPlot(lensesTree)
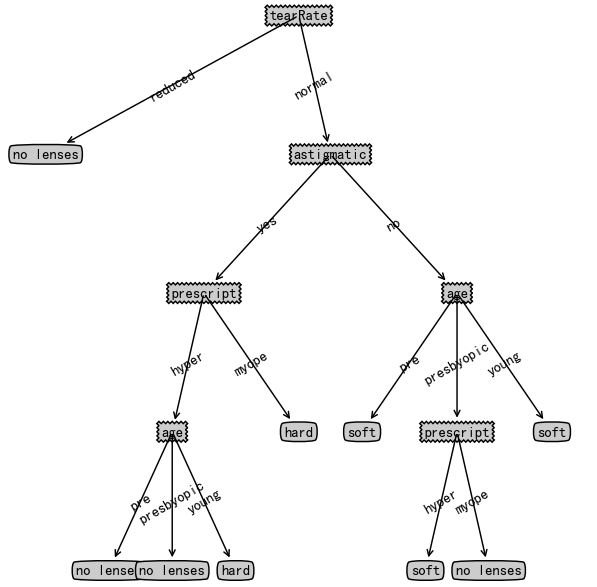
上图中决策树非常好地匹配了实验数据,但这些匹配项太多了,这种称为过拟合(overfitting) 。为了减少过拟合问题,我们可以剪裁决策树,去掉不必要的叶子节点。后面第九章将会学习另一个决策树构造算法CART。