Fisher线性判别与线性判别分析

目录

1. PCA模型
2. FLD模型
2.1. 二分类问题
 2.2. 多分类问题
 2.3. Fisher与贝叶斯决策的关系
 2.4. Fisher与最小二乘法的关系
 3. 瑞利商与广义瑞利商
4. LDA算法小结
5. PCA模型与FLD模型的对比
6. FLD模型的应用实例

PCA模型

未完待续

FLD模型

FLD模型，即Fisher’s Linear Discriminant——Fisher线性判别分析。Fisher判别分析是线性判别分析(Linear Discriminant Analysis， LDA模型)的一种，但线性判别分析不仅限于Fisher判别分析。在周志华《机器学习》书中3.4节讲到的线性判别分析即Fisher判别。

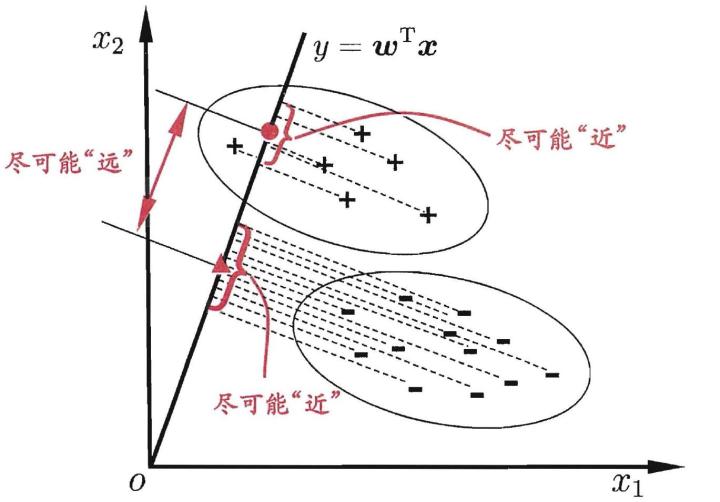
Fisher判别分析的目的：给定一个投影向量$w$，将$x$投影到$w$向量上，使得不同类别的$x$投影后的值$y=w^{T}x$尽可能互相分开(far apart)。

投影向量的选择很关键，当投影向量选择不合理时，不同类别的$x$投影后的$y$根本无法被分开。所以要找到最优的投影向量，使得投影后的值被最大限度地区分。

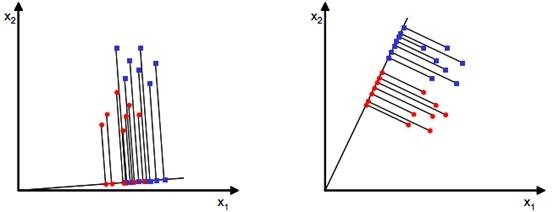
这里的前提是：原始数据是线性可分的。

最大限度的划分投影后的值需要用到两个准则：

投影后的两类样本均值之间的距离尽可能大
投影后两类样本各自的方差尽可能小

二分类问题

对于训练集数据${(x_{i}, c_{i})}, i=1,…,N$，其中$c_{i} \in {1, 2}$。
假设$X_{1} = { x_{i}|1 \le i \le N, c_{i}=1}$, $X_{2} = {x_{i}|1 \le i \le N, c_{i}=2}$。
$N_{1}=|X_{1}|:$ size of subset $X_{1}$，$N_{2}=|X_{2}|:$ size of subset $X_{2}$。
假定投影向量$w$满足$|w|=1$，投影后的样本向量为$y_{i}=w^{T}x, i=1,…,n$。
$Y_{1} = { y_{i}|1 \le i \le N, c_{i}=1}$, $Y_{2} = {y_{i}|1 \le i \le N, c_{i}=2}$。

注意在二分类中，$y = w^Tx$，其中y为一个标量，w和x均为向量。

原样本空间的均值向量为

$m_{k}=\frac{1}{N_{k}} \sum_{x \in X_{k}} x, k \in \{1, 2\}$

投影后的样本均值为

$\tilde{m}_{k} = \frac{1}{N_{k}} \sum_{y \in Y_{k}} y = \frac{1}{N_{k}} \sum_{x \in X_{k}} w^{T}x$ $\tilde{m}_{k} = w^{T}m_{k}, k \in \{1, 2\}$

原样本空间的样本方差为

$s_{k}^{2} = \frac{1}{N_{k}} \sum_{x \in X_{k}} (x - m_{k})^{2}, k \in \{1, 2\}$

原样本空间的协方差矩阵为

$C_{1} = \frac{1}{N_{1}}\sum_{x \in X_{1}}(x - m_{1})(x - m_{1})^{T}$ $C_{2} =\frac{1}{N_{2}} \sum_{x \in X_{2}}(x - m_{2})(x - m_{2})^{T}$

投影后的样本方差为

$\tilde{s}_{k}^{2} = \frac{1}{N_{k}} \sum_{y \in Y_{k}} (y - \tilde{m}_{k})^{2}, k \in \{1, 2\}$

注意

$\| \tilde{m}_{1} - \tilde{m}_{2} \| = \| w^{T}m_{1} - w^{T}m_{2}\| = \|w^T\| \|m_{1} - m_{2}\|= \|m_{1} - m_{2} \|$ 。

Fisher准则函数即求解下式：

$max \frac{|\tilde{m}_{1} - \tilde{m}_{2}|}{\tilde{s}_{1}^{2} + \tilde{s}_{2}^{2}}$

也可以将方差中的系数$\frac{1}{N_{k}} $去掉，也不会影响最终求解的投影向量$w$。

定义$X_{1}$和$X_{2}$中的类内散度矩阵。

$S_{1} = \sum_{x \in X_{1}}(x - m_{1})(x - m_{1})^{T}$ $S_{2} = \sum_{x \in X_{2}}(x - m_{2})(x - m_{2})^{T}$

则散度矩阵(Scatter Matrix)与协方差矩阵(Covariance Matrix)的关系为：

$S{1} = N_{1}C_{1}, S_{2} = N_{2}C_{2}$

则Fisher准则函数还可以写成以下形式：

$max \frac{|\tilde{m}_{1} - \tilde{m}_{2}|^{2}}{\tilde{s}_{1}^{2} + \tilde{s}_{2}^{2}}$ $= max \frac{(\tilde{m}_{1} - \tilde{m}_{2})^{2}}{\tilde{s}_{1}^{2} + \tilde{s}_{2}^{2}}$ $= max \frac{(w^{T}m_{1} - w^{T}m_{2})^{2}}{\sum_{x \in X_{1}}(w^{T}x - w^{T}m_{1} )^{2} + \sum_{x \in X_{2}}(w^{T}x - w^{T}m_{2} )^{2} }$ $= max \frac{w^{T}(m_{1} - m_{2})(m_{1} - m_{2})^{T}w}{w^{T}\sum_{x \in X_{1}}(x - m_{1} )^{2}w + w^{T}\sum_{x \in X_{2}}(x - m_{2} )^{2}w}$ $= max \frac{w^{T}(m_{1} - m_{2})(m_{1} - m_{2})^{T}w}{w^{T}(S_{1}+S_{2})w}$

定义$S_{W} = S_{1} + S_{2}$， $S_{B} = (m_{1} - m_{2})(m_{1} - m_{2})^T$，则准则函数可以重新写成：

$J(w) = \frac{w^{T}S_{B}w}{w^{T}S_{W}w}$

我们把$S_W$称为总类内散度矩阵(Within-class scatter matrix)，它与样本的样本协方差矩阵成正比，并且是对称半正定的。当n>d时，$S_{W}$通常是非奇异的。相似地，$S_B$被称为总类间散度矩阵(Between-class scatter matrix)，也是对称半正定的。$S_B$矩阵最多是秩1矩阵。

$S_B= (m_1−m_2)(m_1−m_2)^T$: measures how scattered is the original input dataset within each class.
$S_W=S_1+S_2$: measures how scattered it is between different classes.

在数学和物理上，把准则函数$J(w) = \frac{w^TS_Bw}{w^TS_Ww}$称为瑞利商。

对于二分类问题，$w^TSw$是一个数字。利用矩阵迹的性质tr(AB)=tr(BA)可得，

$w^{T}Sw=tr(w^{T}Sw)=tr((ww^{T})S)=\sum_{i,j}(ww^{T})_{ij}S_{ij}$

同理，在后文的多分类问题中，

$tr(W^{T}SW)=tr((WW^{T})S)=\sum_{i,j}(WW^{T})_{ij}S_{ij}$

其中，$ww^{T}$和$WW^{T}$都是实对称矩阵。

为了求解$w = argmax J(w)$，则根据最优化理论可知：

$\frac{\partial{J}}{\partial{w}} = \frac{2(w^{T}S_{W}w)S_Bw - 2(w^{T}S_{B}w)S_{W}w}{(w^{T}S_{W}w)^{2}}$

令$\frac{\partial{J}}{\partial{w}} = 0$得，

$(w^{T}S_{W}w)S_Bw = (w^{T}S_{B}w)S_{W}w$

即

$S_Bw = \frac{(w^{T}S_{B}w)}{(w^{T}S_{W}w)}S_{W}w$

在这里$S_Bw = J(w)S_Ww$，我们可以发现$J(w)$不仅是优化的目标函数，而且是矩阵$S_W^{-1}S_B$的特征值(如果$S_W$非奇异)。这属于一个广义特征值(generalized eigenvalue)问题。
上述问题即可转换为：

$S_W^{-1}S_Bw = \lambda w$

我们在maxmize $J(w)$的时候，即求解矩阵$S_W^{-1}S_B$的最大特征值。但这里没必要直接计算
矩阵$S_W^{-1}S_B$的特征值和特征向量。注意矩阵$S_W^{-1}S_B$不一定是对称阵，因此得到的K个特征向量不一定正交，这也是与PCA不同的地方。

将上式变形得到：

$S_W^{-1}(m_{1}-m_{2})(m_{1}-m_{2})^Tw = \lambda w$

由于$(m_{1}-m_{2})^Tw$是标量，所以取w的方向为$w = S_W^{-1}(m_1 - m_2)$。

FLD算法执行步骤如下：

另一种优化的方法。观察观察代价函数 J ，它只与直线 w 的方向有关（与其长度无关， $\alpha w$ 和 w 的 J 值一样），不妨令 $w^TS_ww=1$ ，将优化问题转化为：

$min_w - w^TS_Bw \\ s.t. w^TS_Ww=1$

然后由拉格朗日乘子法，上式等价于

$S_Bw = \lambda S_Ww$

其中，$\lambda$是拉格朗日乘子。注意到$S_Bw$的方向恒为$\mu_0 - \mu_1$，不妨令：

$S_Bw = \lambda (\mu_0 - \mu_1)$

则可得：

$w = S_{w}^{-1}(\mu_0 - \mu_1)$

这里有一点疑问，为什么可以将J(w)转换成上述的带约束的最优化问题？

多分类问题

在多分类问题中，假设总的类别数为C。

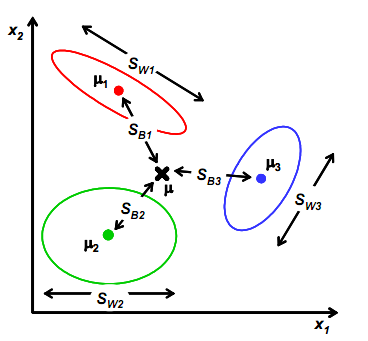
首先引入了总体均值向量$m$和全局散度矩阵$S_T$：

$m = \frac{1}{N} \sum_{x} x = \frac{1}{N} \sum_{i = 1}^{C}N_{i}m_{i}$ $S_T = \sum_{x} (x - m)(x - m)^T$

下面开始推导，

$S_{T} = \sum_{x} (x - m)(x - m)^T \\ = \sum_{i = 1}^{C} \sum_{x \in N_{i}} (x - m_{i} + m_{i} - m)(x - m_{i} + m_{i} - m)^T \\ = \sum_{i = 1}^{C} \sum_{x \in N_{i}} (x - m_{i})(x - m_{i})^T + \sum_{i = 1}^{C} \sum_{x \in N_{i}} (x - m_{i})(m_{i} - m)^T \\ + \sum_{i = 1}^{C} \sum_{x \in N_{i}} (m_{i} - m)(x - m_{i})^T + \sum_{i = 1}^{C} \sum_{x \in N_{i}} (m_{i} - m)(m_{i} - m)^T$

由于$\sum_{x \in N_{i}} x = N_{i} m_{i}$，即$\sum_{x \in N_{i}} (x - m_{i}) = 0$，则上式的中间两项均为0。所以

$S_{T} = \sum_{i = 1}^{C} \sum_{x \in N_{i}} (x - m_{i})(x - m_{i})^T + \sum_{i = 1}^{C} \sum_{x \in N_{i}} (m_{i} - m)(m_{i} - m)^T$ $= S_{W} + \sum_{i = 1}^{C} \sum_{x \in N_{i}} (m_{i} - m)(m_{i} - m)^T$

则定义多分类情况下的类内散度矩阵$S_B$为：

$S_{B} = \sum_{i = 1}^{C} \sum_{x \in N_{i}} (m_{i} - m)(m_{i} - m)^T$

且满足

$S_T = S_W + S_B$

对比二分类的类内散度矩阵$S_B = (m_1 - m_2)(m_1 - m_2)^T$，新定义的类内散度矩阵

$\tilde{S_B} = N_1(m_1 - m)(m_1 - m)^T + N_2(m_2 - m)(m_2 - m)^T$
$= N_1(m_1 - m_2 + m_2 - m)(m_1 - m_2 + m_2 - m)^T + N_2(m_2 - m_1 + m_1 - m)(m_2 - m_1 + m_1 - m)$
$= N_1(m_1 - m_2)(m_1 - m_2)^T + N_1(m_1 - m_2)(m_2 - m)^T + N_1(m_2 - m)(m_1 - m_2)^T \\ + N_1(m_2 - m)(m_2 - m)^T + N_2(m_1 - m_2)(m_1 - m_2)^T + N_2(m_2 - m_1)(m_1 - m)^T \\ + N_2(m_1 - m)(m_2 - m_1)^T + N_2(m_1 - m)(m_1 + m)^T$
$= (N_1+N_2)(m_1 - m_2)(m_1 - m_2)^T + N_1(m_1 - m_2)(m_2 - \frac{N_1m_1+N_2m_2}{N})^T \\$
$+ N_1(m_2 - \frac{N_1m_1+N_2m_2}{N})(m_1 - m_2)^T + N_1(m_2 - \frac{N_1m_1+N_2m_2}{N})(m_2 - \frac{N_1m_1+N_2m_2}{N})^T$
$+ N_2(m_2 - m_1)(m_1 - \frac{N_1m_1+N_2m_2}{N})^T + N_2(m_1 - \frac{N_1m_1+N_2m_2}{N})(m_2 - m_1)^T$
$+ N_2(m_1 - \frac{N_1m_1+N_2m_2}{N})(m_1 - \frac{N_1m_1+N_2m_2}{N})^T$
$= N(m_1 - m_2)(m_1 - m_2)^T - \frac{2N_1^2}{N}(m_1 - m_2)(m_1 - m_2)^T + \frac{N_1^3}{N^2}(m_1 - m_2)(m_1 - m_2)^T$
$- \frac{2N_2^2}{N}(m_1 - m_2)(m_1 - m_2)^T + \frac{N_2^3}{N^2}(m_1 - m_2)(m_1 - m_2)^T$
$= (N - \frac{2N_1^2+2N_2^2}{N}+\frac{N_1^3+N_2^3}{N^2})(m_1-m_2)(m_1-m_2)^T$
$=\frac{2N_1^3 + 2N_2^3 + 3N_1^2N_2 + 3N_1N_2^2 - 2N_1^3 - 2N_1^2N_2 - 2N_1N_2^2 - 2N_2^3}{N^2}(m_1 - m_2)(m_1 - m_2)^T$
$= \frac{N_1^2N_2+N_1N_2^2}{N^2}(m_1 - m_2)(m_1 - m_2)^T$
$= \frac{N_1N_2}{N}(m_1 - m_2)(m_1 - m_2)^T$
即多元分类的类内散度矩阵$\tilde{S}_B$在二分类情况下是原有二分类情况下的类内散度矩阵$S_B$的$\frac{N_1N_2}{N}$倍。

在多分类情况下的投影是从d维空间向(C-1)维空间投影，每一个投影方程为

$y_{i} = w_{i}^Tx, i = 1,\dots,C-1$

用矩阵形式表示即为：

$y = W^Tx$

注意上式中x和y均为向量，W为投影矩阵。

则定义

$\tilde{m}_{i} = \frac{1}{n_{i}} \sum_{y \in Y_{i}} y$ $\tilde{m} = \frac{1}{n_{i}} \sum_{i = 1}^{C} N_i \tilde{m}_{i}$ $\tilde{S}_W = \sum_{i = 1}^{C} \sum_{y \in Y_{i}} (y - \tilde{m}_{i})(y - \tilde{m}_{i})^T$ $\tilde{S}_B = \sum_{i = 1}^{C} N_i (\tilde{m}_{i} - \tilde{m})(\tilde{m}_{i} - \tilde{m})^T$

又已知

$S_{W} = \sum_{i = 1}^{C} \sum_{x \in N_{i}} (x - m_{i})(x - m_{i})^T$ $S_{B} = \sum_{i = 1}^{C} \sum_{x \in N_{i}} (m_{i} - m)(m_{i} - m)^T$ $S_T = S_W + S_B$

则易证

$\tilde{S}_W = W^TS_{W}W$ $\tilde{S}_B = W^TS_{B}W$

多分类问题的实现只要使用$S_T$，$S_W$，$S_B$中的任何两个即可求解。常用的一种实现的优化目标如下：

$max_{W} \frac{tr(W^TS_BW)}{tr(W^TS_WW)}$

其中，$W$是$d \times (C - 1)$维的矩阵，d表示指标特征的维数，tr表示矩阵的迹。
上述问题可以转化为广义特征值问题，即

$S_BW = \lambda S_WW$

则W的闭解为$S_W^{-1}S_B$的(C-1)个最大广义特征值对应的特征向量组成的矩阵。

思考这里为什么要用矩阵的迹？迹和向量场散度的关系？

Fisher与贝叶斯决策的关系

当条件概率密度函数$p(x|\omega_{i})$是多元正态函数，并且各个类别的协方差矩阵$\Sigma$相同时，我们能够直接计算这个阈值。
根据贝叶斯决策计算出的最佳决策边界方程为：

$w^{T}x + w_{0} = 0$

其中，

$w = \Sigma^{-1}(\mu_{1} - \mu_{2})$

并且$w_{0}$

Fisher与最小二乘法的关系

瑞利商与广义瑞利商

瑞利商(Rayleigh quotient)是指这样的函数$R(A,x)$:

$R(A,x)=\frac{x^HAx}{x^Hx}$

其中x为非零向量，而A为$n \times n$的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵，即$A^H=A$。如果我们的矩阵A是实矩阵，则满足$A^T=A$的矩阵即为Hermitan矩阵。

瑞利商R(A,x)有一个非常重要的性质，即它的最大值等于矩阵A最大的特征值，而最小值等于矩阵A的最小的特征值，也就是满足

$\lambda_{min} \le \frac{x^HAx}{x^Hx} \le \lambda_{max}$

具体的证明这里就不给出了。当向量x是标准正交基时，即满足$x^Hx=1$时，瑞利商退化为：$R(A,x)=x^HAx$，这个形式在谱聚类和PCA中都有出现。
以上就是瑞利商的内容，现在我们再看看广义瑞利商(Generalized Rayleigh quotient)。广义瑞利商是指这样的函数$R(A,B,x)$:

$R(A,B, x)=\frac{x^HAx}{x^HBx}$

其中x为非零向量，而A,B为$n \times n$的Hermitan矩阵。B为正定矩阵。它的最大值和最小值是什么呢？其实我们只要通过将其通过标准化就可以转化为瑞利商的格式。
对于Hermite正定矩阵A，存在矩阵B满足$A=BB$,即$A=B^2$,那个我们可以把B写作：$B=A^{\frac{1}{2}}$, 对于B，如果我们求出它的逆矩阵$B^{−1}$,那么就可以表示为：$B^{−1}=A^{−\frac{1}{2}}$

令$x = B^{-\frac{1}{2}}x^{\prime}$，则分母可以写作

$x^HBx = x^{\prime H}(B^{- \frac{1}{2}})^{H}BB^{- \frac{1}{2}}x^{\prime} = x^{\prime H}B^{- \frac{1}{2}}BB^{- \frac{1}{2}}x^{\prime} = x^{\prime H}x^{\prime}$

分子转化为：

$x^HAx = x^{\prime H}B^{- \frac{1}{2}}AB^{- \frac{1}{2}}x^{\prime}$

则我们就把$R(A,B,x)$转化成了$R(A,B,x^{\prime})$：

$R(A,B,x^{\prime}) = \frac{x^{\prime H}B^{- \frac{1}{2}}AB^{- \frac{1}{2}}x^{\prime}}{x^{\prime H}x^{\prime}}$

利用前面的瑞利商的性质，我们可以很快的知道，$R(A,B,x)$的最大值为矩阵$B^{-\frac{1}{2}}AB^{−\frac{1}{2}}$的最大特征值，或者说矩阵$B^{-1}A$的最大特征值，而最小值为矩阵$B^{-1}A$的最小特征值。

谱聚类也使用了类似的方法对矩阵进行标准化。

LDA算法小结

LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在我们进行图像识别图像识别相关的数据分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点。

LDA算法的主要优点有：

在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

LDA算法的主要缺点有：

LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
LDA可能过度拟合数据。

PCA模型与FLD模型的对比

PCA实质上是在寻找一个子空间。而这个子空间是协方差矩阵的特征空间(特征向量对应的空间)，选取特征值最大的k个特征向量组成的特征子空间(相当于这个子空间有k维，每一维代表一个特征，这ｋ个特征基本可以涵盖90%以上的信息)。

Fisher判别和PCA是在做类似的一件事，都是在找子空间。不同的是,PCA是找一个低维的子空间，样本投影在这个空间基本不丢失信息。而Fisher是寻找这样的一个空间，样本投影在这个空间上，类内距离最小，类间距离最大。

FLD属于有监督的降维方法,降维之后的特征具有较好的判别性,与label的相关性较高,而PCA的目的是为了尽可能保留特征的信息,PCA中的一种优化策略就是最小化重构误差。

FLD判别模型是LDA算法的一种。LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。
首先我们看看相同点：

两者均可以对数据进行降维。
两者在降维时均使用了矩阵特征分解的思想。
两者都假设数据符合高斯分布。

我们接着看看不同点：

LDA是有监督的降维方法，而PCA是无监督的降维方法
LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
LDA除了可以用于降维，还可以用于分类。
LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

LDA模型的应用实例

Reference

https://www.cnblogs.com/pinard/p/6244265.html
https://www.cnblogs.com/txg198955/p/4106682.html
https://zhuanlan.zhihu.com/p/33742983
http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024384.html
http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024389.html

Fisher线性判别与线性判别分析